Rockin' around the BGP Trie
An efficient data structure to perform a simple CIDR lookups
December 30, 2023
This article is marked as a learning article meaning that this article was written for the sake of me learning through explaining.
As such, please take the content in this article with a grain of salt. Feel free to include any comments that might correct something incorrect I have said.
BGP is a cool antiquated technology that powers routing
stuff all over the internet. The basic idea is simple: a router
tells other routers that it should route traffic to a destination
based on some rules. The rules are assigned to some prefix or
CIDR (they are notated like 10.99.0.0/24).
If you know about IPv4, you’ll know that you can actually represent
every IPv4 address as a 32 bit integer, so a CIDR notation is literally
a prefix that is n bits long (indicated by the /n part).
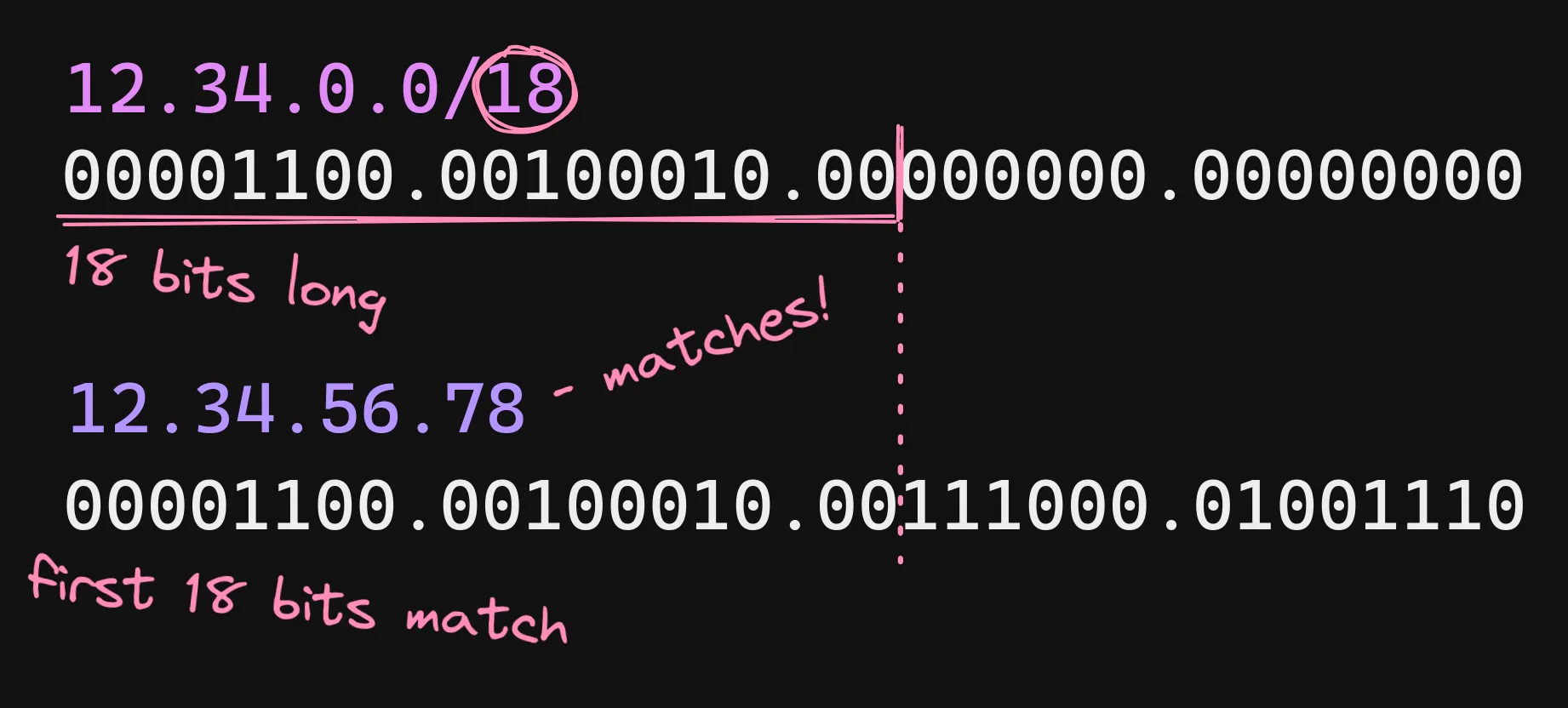
This is pretty useful for one big thing: finding out which operators are
associated with a specific IP address. As an example, as of the time of
writing this, one of the CIDR prefixes that Cloudflare
announces is
1.1.1.0/24 for their famous 1.1.1.1 DNS service.
Since the prefix’s length is 24 bits, that means there is 8 bits at the
end of the address that can be changed. Because , that means
this CIDR covers 256 addresses that being 1.1.1.0 to 1.1.1.255.
This means if we have a list of all the published prefixes, we can take
an IP address like 1.1.1.128 and go through each prefix to see if it matches.
Eventually, we will end up finding the 1.1.1.0/24 prefix published by
Cloudflare. With that, we can conclude that 1.1.1.128 belongs to Cloudflare.
BGP.tools provides a way to get the a visibility table with ASNs through
their API . As of writing this,
running cat -v table.txt | wc -l yields 1,217,754 prefixes! That’s a lot
of prefixes but includes both IPv4 and IPv6. Filtering to just IPv4 using
grep -v -F ':' table.txt | wc -l gives 1,006,324. This is a perhaps more
managable number.
Writing it in Zig
What we’re writing here today is a trie. A trie is a tree that enables fast prefix searches. The reason why this works is because it iterates over the IP bit by bit and chooses a side of the tree (zero or one) and follows it to the next node. In practice, this is rather fast.
Let’s start off by writing a node struct for each vertex in our trie (tree) graph.
pub const TrieNode = struct {
// 0 or 1 to lead to the next bit (node)
zero: ?*TrieNode,
one: ?*TrieNode,
// an IP can have more than 1 ASN
asns: ?[]i32,
fn blank() @This() {
return .{ .zero = null, .one = null, .asns = null };
}
};
Next is some boilerplate to define the trie as a whole, a TrieParent.
const std = @import("std");
const ArenaAllocator = std.heap.ArenaAllocator;
const Allocator = std.mem.Allocator;
pub const TrieParent = struct {
arena: ArenaAllocator,
root: TrieNode,
// a beginner mistake in Zig is passing another arena's
// `arena.allocator()` into a new ArenaAllocator.
// don't do that! it'll segfault immediately.
pub fn init(allocator: Allocator) @This() {
return .{
.arena = ArenaAllocator.init(allocator),
.root = TrieNode.blank(),
};
}
pub fn deinit(self: @This()) void {
self.arena.deinit();
}
};
All that’s left now is to write some insertion and querying functions.
This is all inside the TrieParent struct.
// insert an item into the trie given an ip
// and a length the asn is associated data
pub fn insert(self: *@This(), ip: u32, length: u5, asn: i32) !void {
const allocator = self.arena.allocator();
var current_node = &self.root;
// the shift is how many bits from the left we are in
// 0 meaning we are starting at the leftmost bit and going
// rightward until we reach the desired length
var shift: u5 = 0;
while (shift < length) {
// checks if the shift(th) bit from the left is 1 or 0,
// get the corresponding node from the current node
// as a pointer (so that if it is null we can set the
// pointer's value to a pointer to a valid new TrieNode)
const node = if (ip >> (31 - shift) & 1 == 0)
¤t_node.zero
else
¤t_node.one;
// if the node isn't null, set the current node and
// shift another bit rightwards and continue
if (node.*) |n| {
current_node = n;
shift += 1;
continue;
}
// otherwise we have to create a new node to place there
const new_node = try allocator.create(TrieNode);
new_node.* = TrieNode.blank();
node.* = new_node;
current_node = new_node;
shift += 1;
}
// now that we've reached the desired node we can add our data
// if there's already an ASN there, we need to expand the array
if (current_node.asns) |asns| {
// allocate the same array but one longer
const new_asns = try allocator.alloc(i32, asns.len + 1);
// copy the old content over
@memcpy(new_asns[0..asns.len], asns);
// set the last item to the new ASN
new_asns[asns.len] = asn;
// free the old array
allocator.free(asns);
// sort the array for future optimizations...
std.sort.insertion(i32, new_asns, {}, std.sort.asc(i32));
// set the asns to the new array
current_node.asns = new_asns;
return;
}
// otherwise since there's no array here we can just allocate
// one and set the array's singlular value to the asn and
// set the node's asn array to the pointer.
const new_asns = try allocator.alloc(i32, 1);
new_asns[0] = asn;
current_node.asns = new_asns;
}
pub fn query(self: @This(), ip: u32) ?[]i32 {
var current_node = &self.root;
// same concept as the last but since we can count up
// instead of counting down we can just count backwards
var shift: u5 = 31;
var least_specific = current_node.asns;
while (shift > 0) {
const node = if (ip >> shift & 1 == 0)
current_node.zero
else
current_node.one;
// if the node exists go deeper
// otherwise give up
if (node) |n| {
if (n.asns) |asns| least_specific = asns;
current_node = n;
} else {
return least_specific;
}
shift -= 1;
}
return least_specific;
}
Ok that wasn’t the best implementation. I’ll follow this post up and link it here when it’s complete for all the optimizations I came up for this.